Minimering av logiska funktioner

Minimering av booleska funktioner , allt du behöver veta , hur man minimerar booleska funktioner . Minimering av logiska funktioner tillämpas med vissa metoder såsom – med hjälp av booleska algebraregler , med hjälp av Karnaugh-kartor , Qines metod (Mc clues, Presto, Espresso) – för datorer, räknemaskiner .Varje metod har sitt eget förfarande och sin egen lösning . 

Läs också :  Koppling av uttag 

Minimering av logiska funktioner

Använda metoder för minimering

1. Användning av booleska algebraregler – lämplig för enkla funktioner

2. Användning av Karnaugh-kartor

3. Qines metod (Mc clues, Presto, Espresso) – för datorer, räknemaskiner

Regler för boolesk algebra och deras användning för minimering av booleska funktioner

om vi ersätter loggskyltarna i reglerna. produkt och summa (+ och * ), värdena 0 och 1 ( om sådana finns) , får vi en ny giltig regel.

Kommutativ lag (substitution)

A+ B = B+ A A*B= B*A

Associationsrätt ( association)

A + (B + C) = (A+B)+C A*(B*C)= A*B)*C

Distributiv lag (multiplikation)

A*(B+C)= A*B+A*C A+(B*C)= (A+Bn*(A+C)

Minimering med Karnaugh-karta -Minimering av logiska funktioner

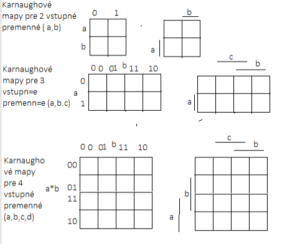
Karnaugh-karta – Grafisk loggning. Funktioner

– Den har en kvadratisk eller rektangulär form som, i fallet med ,,n” opartiska variabler, har ,,2″ celler

– En sanningstabellstatusrad tilldelas varje fält och värdet för utmatningen ,,Y” anges i det fältet

– Användning av kartor är lämplig för högst sex variabler.

– Förenkling med hjälp av dessa kartor respekterar följande grundläggande regler:

a+a(negation)=1

a+a = a

Extrahera algebraisk formfunktion från karta

Exempel:

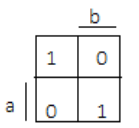
Skriv ner den algebraiska funktion som ges av Karnaugh-kartan:

Lösning:

1. ÚNDF (fullständig normal disjunktiv form)

Vi skriver funktionen på samma sätt som sanningstabellen med summan av basloggarna. produkter.

Vi listar de rutor där funktionen har värdet 1:

-1. kvadrat: A=0,B=0- bas logisk produkt A( neg) * B( neg)

4. Kvadrat A = 1,B = 1 – z=acladn=y logisk produkt A*B

– resulterande funktion: A( neg) * B (neg) + A*B)

2. ÚNKF (fullständigt normal konjunktival form)

Den här gången tittar vi på kvadrater där funktionen antar värdet 0 och använder notationen produkt av baslog. produkter.

-2. kvadrat A= 0,B=1 – besvärjelse. Logg. summan av A+B( neg)

-3. fyrkantig : A= 1,B=0- incantation. Logg. summan av A(neg)+B

– Resulterande funktion : ( A(neg)+B) * ( A*B(neg) )

Är svett farligt för håret? Hur motverkar man det?